积分学是高等数学的主要模块之一，在积分中很多情况下需要对变积分限的函数进行求导运算，例如，求变限积分函数极限时运用洛必达法则、求含变限积分且以参数形式表示的函数的导数、积分等式和不等式的证明等问题，这些情况不仅会出现在定积分中，而且有时也会出现在重积分中，下面我们对重积分中变限积分函数的求导方法做些分析介绍，供考研复习和学习高等数学的同学参考。

　　一、重积分变限积分函数的求导方法

　　在二重积分或三重积分中，如果含有变积分限，当需要对变积分限中的变量求导时，可以通过引入辅助函数等方法，将重积分化为关于辅助函数的定积分，然后利用定积分中的对变积分限函数的以下求导公式进行求导计算：

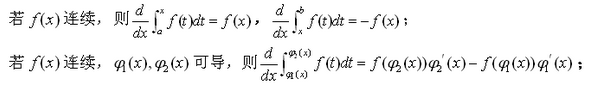
　　当被积函数中含有求导变量时，应先用换元法或提出因式，使被积函数中不含求导变量，然后再用上述方法对变限积分的函数进行求导。

　　二、典型题型分析

　　通过上面的分析和例题看到，在重积分中很多情况下都会用到变限积分函数的求导公式，例如求含二重积分的函数极限、偏导数的计算、重积分等式或不等式的证明等，计算或证明中常把重积分转化成或看作定积分来求导，必要时须交换积分次序，求极限时常结合洛必达法则和等价无穷小代换等方法，同学们在解答考研数学中类似问题时要灵活运用所学的各种知识。